本帖最后由 snowfly 于 15-10-22 11:05 编辑 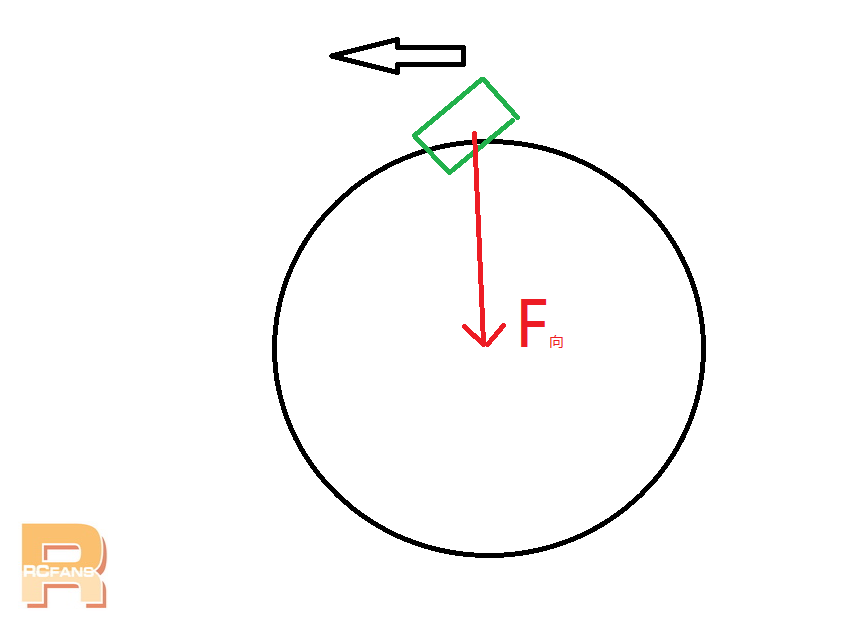
以绕圆周飘移为例开始说明,车辆运动方向如箭头所示,车辆所受合力即为向心力“F向”,“F向”大小、方向发生变化车体运动轨迹就会改变 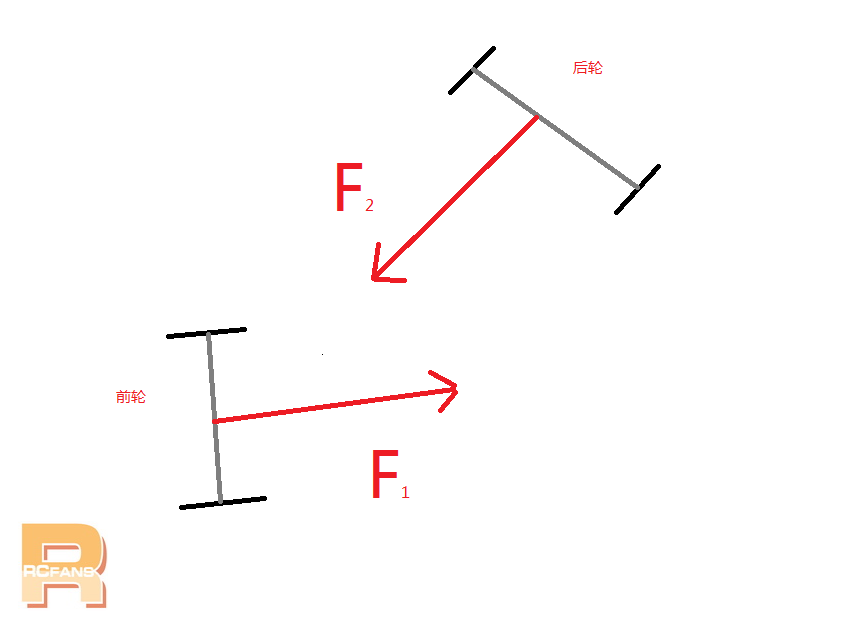
放大车体看前后轮受力,前轮受到地面给的摩擦力F1,后轮受到驱动力与摩擦力的合力F2 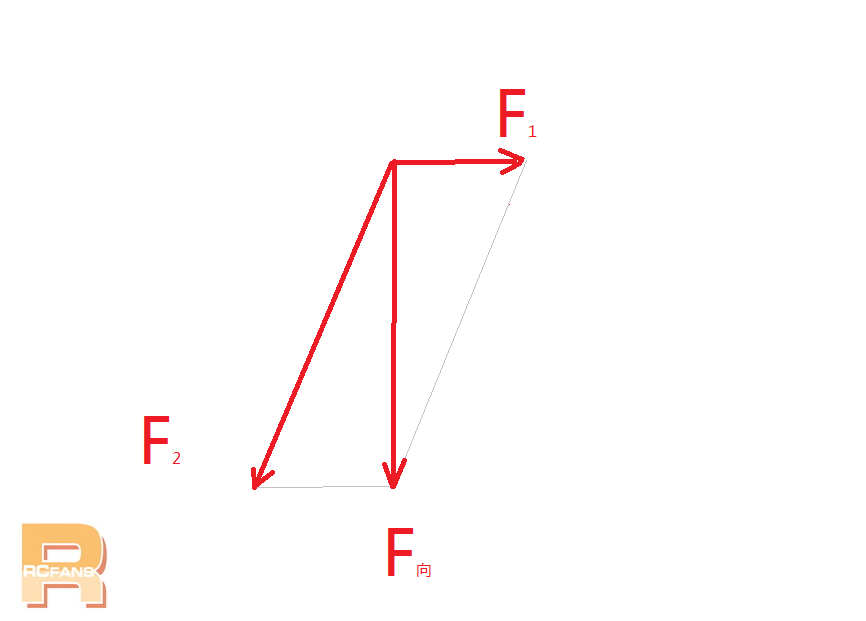
力学平行四边形法则得出F1、F2合力,必须与“F向”大小相等方向一致,才能绕既定圆周漂移运动。如图可见F1的大小与方向就是是影响车辆绕圆周漂移轨迹的因素之一。而F1与阿克曼角息息相关。 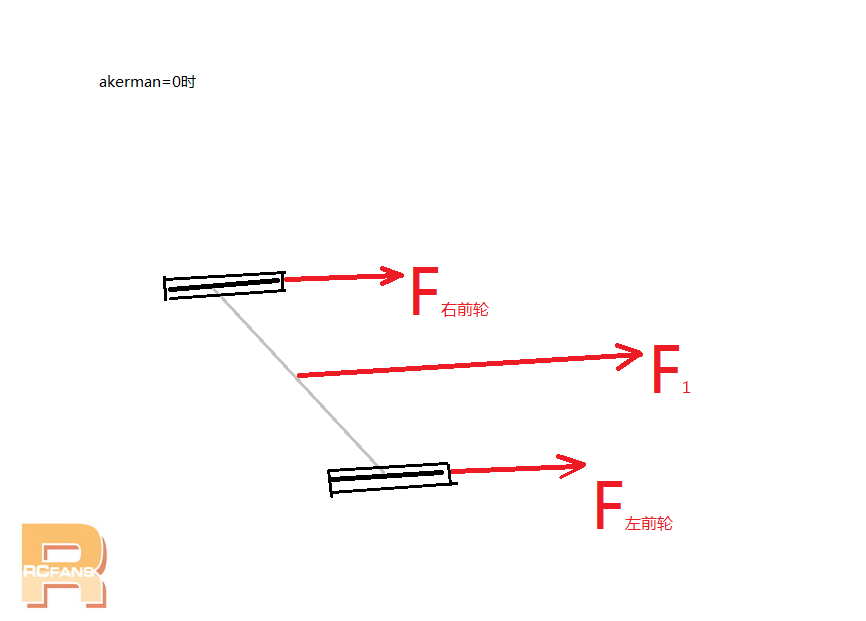
如图当阿克曼角=0时,左右前轮所受摩擦力分别为F右前轮、F左前轮。 “F右前轮”方向与“F左前轮”方向一致。可以用平行四边形法则画出合力F1,“F1”与“F左、F右”方向一致 在这里我们只考虑左右轮在加减速瞬间的重心移动,前后重心移动忽略不计,漂移过程中轮胎是滑动的,我们不妨把轮胎的摩擦力设为滑动摩擦力,滑动摩擦力计算公式F=uN(u为摩擦系数,N为地面给轮胎的压力) 在左右轮重心移动的时候由于车子总质量是不变的,所以“N左前轮+N右前轮”是不变的=N1。F1=F左+F右。更可发现此时无论重心怎么样转移,这个瞬间F1的大小方向都不变。 可见这种结构形式是非常稳定的。漂移时前轮可以非常稳定 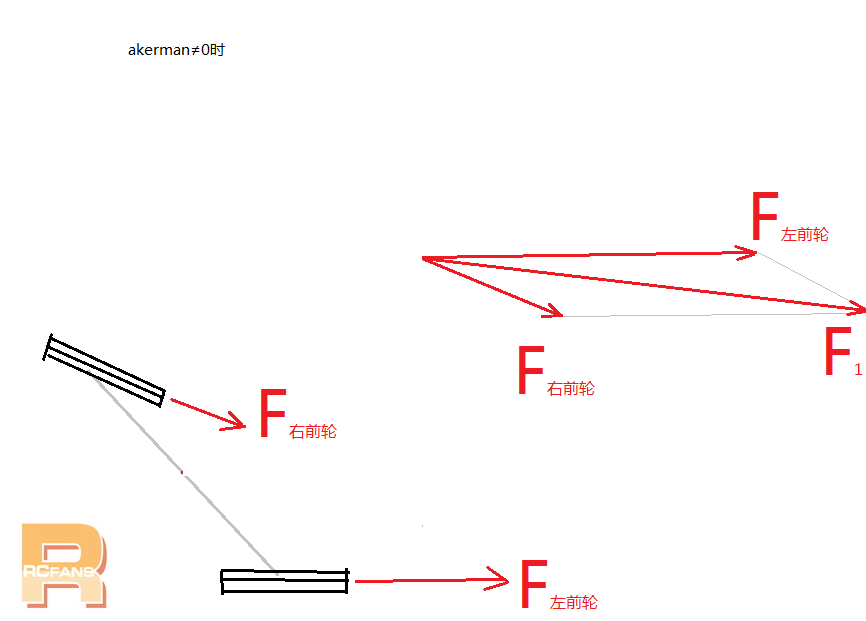
如图当阿克曼角≠0时,左右前轮所受摩擦力分别为F右前轮、F左前轮。 “F右前轮”方向与“F左前轮”方向有夹角θ。接下来同上计算左右轮摩擦力,用平行四边形法则画出合力F1 大家可以有兴趣自己试试画下,对比下就很清楚,当加油门重心偏移到左侧车轮,左侧车轮摩擦力增加,右侧车轮摩擦力减少,左右轮增加减少摩擦力数值相等(画图时即为增加或减少相同长度),当减油门时情况相反。这时观察F1大小与方向均有变化,与后轮所受F2形成的合力“F向”较之阿克曼角=0时无论角度还是大小变化曲线都变大。可以利用这种特性。使车身反应慢的车子反应变快些,反应慢的车子不妨增加一些阿克曼角度 |
广告投放|联系我们|手机|投稿|Archiver|About us|Advertise|遥控迷模型网|RCFans ( 粤ICP备10210518号-1 )
版权所有 RCFans.com © 2003-2016